Sistemas de Ecuaciones Lineales con dos Incógnitas

Curriculum chileno ...
NEM: Segundo Medio.
Eje Temático: I. Álgebra y Funciones.

CMO: 2. Funciones. d. Resolución de Sistemas de Ecuaciones Lineales con 2 Incógnitas. Gráfico de las rectas. Planteo y resolución de problemas y desafíos que involucren sistemas de ecuaciones. Análisis y pertinencia de las coluciones. Relación entre las expresiones gráficas y algebraicas de los sistemas de ecuanciones lineales y sus soluciones.
===============================================

Resolvamos el Sistema de Ecuaciones Lineales con 2 Incógnitas:

Oservaciones:

a) En primer lugar hays 2 ecuaciones ( la 1) y la 2) ).

b) Cada una de ellas vincula 2 incógnitas x e y (o dos variables, una independiente y otra dependiente).

c) Si despejásemos cualquier variable, por ejemplo y=f(x) o incluso x=f(y), en ambos casos se tiene que f(ax)=af(x) ó f(ay)=af(y). Se dice que cuando se cumple esta característica hay linealidad ....

Es por esto que el sistema anterior es un Sistema de Ecuaciones Lineales. Es más, en este caso se habla de un Sistema de 2 x 2 Lineal, porque hay dos ecuaciones y dos incógnitas.

Hay varias formas de resolver un sistema de este tipo:

1) Reducción ; 2) Sustitución; 3) Igualación; 4) Método Gráfico; 5) Método de los Determinantes; 5) Método Matricial.

En este espacio vamos a utilizar los 4 primeros:

Solución por Reducción: Consiste en igualar los coeficientes de alguna de las incógnitas elegida y cambiar el signo en una de las ecuaciones.

Las ecuaciones son: 1) x+2y = 80 ; 3x + 2y = 150

Se multiplica la primera por -3

1) -3x -6y = -240

2) 3x + 2y = 150

Se suman ambas ecuaciones: -4y = -90, de donde sigue que y= 22,5. Si reemplazamos el valor de y en cualquiera de las dos ecuaciones, obtenemos el valor de x.

x + 2(22,5) =80 ; x + 45 = 80 ; x = 80 -45 = 35

Solución por SUSTITUCION: Se despeja una de las incógnitas y se introduce en la otra ecuación,

1) x + 2y = 80

2) 3x + 2y = 150

de 1) x=80-2y y lo ponemos en la segunda ecuación:

3(80-2y) + 2y = 150

240 -6y +2y = 150; -4y = -90 ; y= 22,5 y sigue como en Reducción.

Solución por Igualación: Se despeja la misma incógnitas en las dos ecuaciones y se igualan:

1) x+2y = 80---------> x = 80 -2y

2) 3x + 2y = 150 -----> x = (150-2y)/3

Igualando: 80-2y = (150 -2y)/3

240 - 6y = 150 - 2y y sigue muy similar a los otros dos métodos.

Solución Gráfica: La solución de un sistema de ecuaciones, de existir, debe ser un punto (par ordenado que cumple ambas ecuaciones). Por tanto, si existe, es el punto de la intersección de las dos rectas .... Entonces, si hay solución será aquella se encuentre en la intersección:

Grafiquemos la primera recta:

Grafiquemos la segunda recta:
desde donde se puede verificar la solución (22.5, 35)

Planteo de Problemas:

El perímetro de un rectángulo es A cm. Si el largo se disminuye en 2 cm. y el ancho se aumenta en 2 cm. Resulta un cuadrado. ¿Cuál es el área del cuadrado?

Resolviendo por reducción, por ejemplo llegamos a: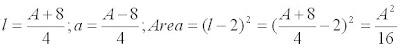

Pertinencia de las soluciones (de la ecuación):