jueves, 31 de julio de 2008
Las "lecciones de la democracia"
Función Cuadrática - Séptimo Posteo - Materia: Intersección con el eje X, casos.
NM3 : Enseñanza Media, tercero Medio:
CMO : I Algebra y Funciones. 2. a. Función Cuadrática. Discusión de los casos de intersección de la parábola con el eje X (abcisas).

miércoles, 30 de julio de 2008
Probabilidad en Espacios Muestrales Infinitos NO ENUMERABLES - usando regla de Laplace (Esto SE PUEDE entender en E. Media)

CMO 2do. Medio: Regla de Laplace, para (micro)eventos equiprobables.
Contenido Extraordinario Tercero Medio: Grafica de regiones planares.
- - - - -
Se puede mirar en este BLOG lo que son los espacios enumerables y no enumerables, a propósito de varios posteor en torno a Cantor (Creo que uno le llamé, copiando un libro: El paraíso de Cantor) .... Pero recordemos algo:
El conjunto de los números pares y el de los impares son INFINITO enumerables puesto que vada uno de sus componentes se puede asociar a uno de los números naturales .... Pero el Conjunto de los números Reales (IR) no es enumerable, no se le puede asociar biunivocamente cada uno de los números naturales, ni si quiera el trazo [0,1] es enumerable, es tan infinito como el conjunto de todos los Reales (hemos puesto algunas imágenes visuales de ello) ....
Para la enseñanza media, se postulan probabilidades invocando conjuntos INFINITOS no enumerables, pero asociados a medidas geométricas finitas tales como LONGITUD, AREA y VOLUMEN.
Así las probabilidades de un evento A serán, en su fórmula Laplaceana:
P= Longitud de A / Longitud de S
P= Area de A / Área de S
P= Volúmen de A / Volúmen de S
Y en general se habla de que este tipo de probabilidades es uniforme.
Un BELLO ejemplo (no fácil):
Sobre la línea R (Reales), se selecciona al azar los puntos a y b tales que -2 <=b<=0 y 0<=a<=3 como se muestra en la figura. Hallar la probabilidad p para que la distancia d entre a y b sea mayor que 3.
 Solución:
Solución: 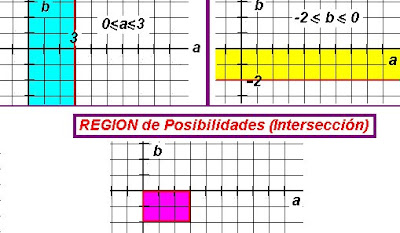
Está dada por todos los pares ordenados que cumplen las restricciones para a y b: -2<=b<=0 ; 0<=a<=3
Veamos ahora los pares ordenados de la región favorable, dados por la región que describe la inecuación d=a-b>3

Probabilidad Pedida=

Función Cuadrática COMPLETA: Sexto Posteo
NM3 : Enseñanza Media, tercero Medio:
CMO : I Algebra y Funciones. 2. a. Función Cuadrática.
En este posteo estudiaremos la función:

con a, b, c distintos de cero. Resolución de segundo grado por completación de cuadrados y su aplicación en la resolución de problemas.
- - - - - - - - - -
Grafiquemos un ejemplo:

Y ahora, usando GRAPHMATICA, grafiquemos:

Esta gráfica nos da una elegante parábola, con sus ramas que se van abriendo hacia el infinito. Pero OJO que hay dos puntos en donde corta el eje de las X. En la gráfica se puede ver que son los pares de puntos (2,0) y (5,0). A estos puntos se les llama Ceros de la Función, porque en cuando la variable dependiente de hace cero, es decir: y= f(x) =0.
Vamos a revisar esto teóricamente y con el ejemplo anterior. Esto se hace completando el cuadrado de binomio. Partamos con el ejemplo:
Hemos encontrado los dos valores para los cuales Y=0, y son junto x=5, x=2, que era lo que observábamos en la gráfica.
Generalicemos lo anterior y encontraremos una fórmula, para x1 y x2 en función de los coeficientes a, b, c. Veamos:
Veamos un caso concreto (Tomado del libro Santillana):
Problema (página 51, tercero medio)Encuentra la base b y la altura h de un triángulo de área 2 metros cuadrados si su base es 3 metros más larga que su altura.
 Y resolvamos esta ecuación por completación de cuadrados:
Y resolvamos esta ecuación por completación de cuadrados:Obviamente, de las dos soluciones, nos sirve h2=1 metro, porque no pueden haber distancias negativas.
Función Cuadrática: Quinto Posteo - Desplazamiento Horizontal
CMO : I Algebra y Funciones. 2. a. Función Cuadrática.




Función Cuadrática: Cuarto Posteo - Desplazamiento Vertical
CMO : I Algebra y Funciones. 2. a. Función Cuadrática.




Función Cuadrática: Tercer Posteo
CMO : I Algebra y Funciones. 2. a. Función Cuadrática.
Ahora vamos a hacer una comparación: vamos a seguir con b=0, c=0 ; pero vamos a hacer que a tome tres valores distintos: a=0,5 ; a= 1 ; a= 3
veamos la Tabla de Valores:

veamos la Gráfica:
 A mayores valores de a, la curva se contrae (se acerca más al eje Y), a menores valores de a, la curva se dilata (se aleja del eje Y) !!!!
A mayores valores de a, la curva se contrae (se acerca más al eje Y), a menores valores de a, la curva se dilata (se aleja del eje Y) !!!!
Función Cuadrática: Segundo Posteo
CMO : I Algebra y Funciones. 2. a. Función Cuadrática.
Y que pasa si el coeficiente a, de una función cuadrática es negativo. Veamos el caso más simple, cuando a=-1; b=0, c=0: es decir, vamos a graficar:

Como el signo menos antecede al cuadtrado, todos los valores de y serán negativos, a excepción del cero. Esto hace que la curva se refleje como en un espejo, se provoca una simetría especular con eje igual a la recta de abcisas.
Tabla de valores pro gráfica:

Y veamos la gráfica, comparativamente a x al cuadrado .....

En Graphmática
"Me gustan los estudiantes" (Violeta Parra)

¡SEREMOS SU PEOR PESADILLA EN TIEMPOS DE ELECCIONES!
Jarro de Agua: Extracto a la entrevista de un Premio Nacional de Literatura .....
martes, 29 de julio de 2008
Función Cuadrática - Contenidos (3ro. Año Medio): Primer Posteo
CMO : I Algebra y Funciones. 2. a. Función Cuadrática. Gráfico de las siguientes Funciones:
 Discusión de los casos de intersección de la parábola con el eje x. Resolución de ecuaciones de segundo grado por completación de cuadrados y su aplicación en la resolución de problemas.
Discusión de los casos de intersección de la parábola con el eje x. Resolución de ecuaciones de segundo grado por completación de cuadrados y su aplicación en la resolución de problemas.(Matemáticas) Programa de estudios de Primer año Medio.
- - - - - - - - - -
Función Cuadrática:
Una Función Cuadrática es una expresión de la forma:
 en donde (único requisito), el cieficiente "a" es distinto de cero.
en donde (único requisito), el cieficiente "a" es distinto de cero."a", "b", "c" son coeficientes numéricos conocidos.
"x" es la variable independiente
"y" es la variable dependiente, aquella que depende de los valores que toma "x".
Dependiendo de los valores que tomen "a", "b", "c", se obtendrán, todas y cada una de las funciones expuestas en la Tabla de Funciones Cuadráticas, presentada más arriba. Para muestra un botón:

Demos algunos valores a la variable independiente (x), para lograr los de la variable dependiente (y):
Tabla de valores PRO gráfica:

Y ahora veamos la gráfica:

Invención del CERO (Tomado de Wikipedia)

Los babilonios escribían en arcilla sin cocer, sobre superficies planas o tablillas. Su notación era cuneiforme. En tablillas datadas en el año 1700 a. C. se ven anotaciones numéricas en su particular forma; este sistema no se parecía al actual de base 10, pues los babilonios utilizaban un sistema en base 60, y con esa notación no era posible distinguir el número 23 del 203 o el 2003. Alrededor del 400 a. C., los babilonios comenzaron a colocar símbolos de dos cuñas en los lugares dónde en nuestro sistema escribiríamos un cero, que en realidad se leía 2”3 (dos, varios, tres). Esta ambigüedad no pareció preocupar a los babilonios.
Jeroglífico maya para el cero, año 36 a. C. Es el primer uso documentado del cero autónomo como se conoce hoy en día.
En el 500, Aryabhata, crea un sistema numérico que no tenía cero y era un simple sistema posicional. Se usó la palabra "kha" para la posición cero y posteriormente el mismo cero adoptaría ese nombre. En ocasiones se usaba un punto en los primeros manuscritos indios para mostrar un espacio vacío en la notación posicional. Pero muchos historiadores objetan estas fuentes como reales del cero al comprobarse que el punto también se usaba para mostrar algo desconocido, lo que usualmente sería una "x" para la Matemática moderna.
El primer registro cierto del uso del cero indio está datado en el año 876. Esta datación es la única en la que hay acuerdo. Los hindúes, lo utilizaron como cifra en el siglo X (900 d. C.), pero fueron los árabes quienes lo introdujeron en Europa.
El primer matemático importante que hizo uso del signo "0", hacia el año 810 de nuestra era, fue el árabe Mohammed ibn Musa al Khwarizmi, cuyos escritos han llegado hasta nuestros días. La palabra "cero" proviene de la traducción de su nombre en sanscrito "shunya" (vacío) al árabe "sifr" (صفر), a través del italiano. La voz española "cifra" también tiene su origen en "sifr".
Volúmen de un cuerpo inscrito en otro ....
Curso: Cuatro Medio
CMO: II. Geometría. a. (...) Resolución de problemas que plantean diversas relaciones entre cuerpos geométricos: por ejemplo, uno inscrito en otro.
Ejercicio:

Calculemos el volúmen de una esfera inscrita en un cubo cuyo volúmen es 125 metros cúbicos.
El radio de la esfera, si esta está perfectamente inscrita en el cubo, es igual a la mitad de la arista del cubo. Si el volúmen del cubo es 125 metros cúbicos, entonces su arista a=5 m. Luego, el radio de la esfera es 5/2 metros. Así:

lunes, 28 de julio de 2008
Comentario histórico sobre la evolución del lenguaje algebraico

CMO Pertinente: Álgebra y Funciones. d. Comentario histórico sobre la evolución del lenguaje algebraico. Primer Año de Enseñanza Media.
Veamos lo que dice sobre el concepto álgebra en WIKIPEDIA:
La palabra «álgebra» deriva del tratado escrito por el matemático persa Muhammad ibn Musa al-Jwarizmi, titulado Al-Kitab al-Jabr wa-l-Muqabala (en árabe كتاب الجبر والمقابلة) (que significa "Compendio de cálculo por el método de completado y balanceado"), el cual proporcionaba operaciones simbólicas para la solución sistemática de ecuaciones lineales y cuadráticas. Etimológicamente, la palabra «álgebra» (también nombrado por los árabes Amucabala) جبر (yebr) (al-dejaber), proviene por lo tanto del árabe y significa "reducción", operación de cirugía por la cual se reducen los huesos luxados o fraccionados (algebrista era el médico reparador de huesos).

Textos del diálogo, en el comix (Ayuda a entender cómo la ciencia renace cuando se acoge la creatividad humana):
"Todos los pueblos que se han preocupado por el avance de las ciencias han creado centros en los que sus sabios pueden trabajar, intercambiar sus ideas ... Como nuestras actuales universidades y academias.
Ahora estamos en el siglo IX de nuestra era, en Bagdad, capital del mundo árabe.
En esta ciudad se reúnen artistas, científicos, escritores ... Aquí se escribieron, bajo el reinado del califa Al Raschid, los cuentos de Las mil y una noches, Aladino y la lámpara maravillosa, Simbad el marino ....
Ahora, el califa (gobernador) de Bagdad es su hijo, Al Mamun. Cuentan que una noche Al mamun tuvo un sueño en el que se le apereció el gran filósofo griego Aristóteles.
Al depertar Al Mamun, impresionado, mandó traducir al árabe todas las obras griegas que se habían encontrado hasta ese entonces. También se mandó construir una Casa de la Sabiduría en la que se pudieran reunir los sabios para estudiar y hacer avanzar la ciencia. Entre ellos estuvo el matemático y astrónomo Al-Juarizmi, uno de los más famosos del mundo árabe."
CONTRIBUCIONES de Al-JUARIZMI
Escribió un primer libro sobre aritmética en el que daba a conocer el sistema de numeración que usaban en India. Tuvo mucho éxito, prueba de ello es que hoy, en pleno siglo XXI recibimos su influencia, pues usamos este sistema de numeración. Muchos lectores empezaron a llamar a esa forma de contar algoritmo o guarismo, que es el propio nombre de Al-Juarizmi mal pronunciado. Su segundo libro también fue un éxito y trataba sobre el álgebra. De hecho la palabra "álgebra" viene precisamente del título del libro, que se llamaba "Al Jabr ...." y un largo título árabe .....
Pequeña nota de Evolución del Lenguaje Algebraico: Período RENACENTISTA ....
La metamorfosis del número 2 -ó- cómo cambiar el número 2 con un .....
Fuente: Matemáticas Divertidas y Curiosas - Malba Taham
¿Cómo puedo, mediante un procedimiento muy simple, convertir el número 2 en el número 3 y la letra M?
(Diapo)
Análisis Curricular:
La actividad se enmarca en la unidad de Transformaciones Insométricas o Isometrías (Unidad 3 según el Programa de estdios del MINEDUC), del Primer Año de Enseñanza Media.
CMO Pertinente: Transformaciones. a. Traslaciones, simetrías y rotaciones de figuras planas. Construcción de figuras por traslación, por simetría y por rotación en 60º, 90º, 120º y 180º.
MATERIA:
Isometría viene del Griego:
Iso = Igual o mismo
Metría = Medir
Isometría: Acción o movimiento o transformación geométrica que deja inalterada la figura en el plano.
Esta es una SIMETRIA AXIAL (Axial: Eje): Es una transformación en la cual cada punto de una figura se asocia a otro punto llamado imagen, que cumple las siguientes condiciones:
1) El punto y su imagen está a igual distancia de una línea recta llamada Eje de Simetría.
2) El segmento que une un punto con su imagen es perpendicular al Eje de Simetría.
Ejercicio 1: ¿Cuál es la figura que viene en la serie?
 En la secuencia vienen 2 números cuatro, uno bien escrito y el otro dibujado simétricamente respecto de una vertical como se indica en la figura de a continuación ....
En la secuencia vienen 2 números cuatro, uno bien escrito y el otro dibujado simétricamente respecto de una vertical como se indica en la figura de a continuación ....
Ejercicio 2: ¿Qué habría que hacer, para dejar el 3 de la anterior presentación (Power Point) tal como lo suamos siempre? Respuesta: Provocar una simetría axial (o especular: de espejo) respecto de un eje vertical a la tangente inferior de (pendiente cero) all número, a cualquier distancia ....

domingo, 27 de julio de 2008
Wolas !!!!
Semestre parte con movilizaciones .....
CAMINATA CON MÚSICA Y ESTUDIANTES DEL LICEO DARÍO E. SALASCUÁNDO: Lunes 28 de julioA QUÉ HORA: Nos juntamos a las 7:30 horas de la mañana DÓNDE: en Avenida España con Alameda, Santiago Centro, Metro República CONVOCAN: MEMORIA FEMINISTA, feministas autónomas junto a diversas organizacionesL@S VAMOS A DEJAR DE VUELTA A CLASES Y A EXPRESAR QUE NO ACEPTAREMOS MÁS REPRESIÓN Y MALOS TRATOS A ESTUDIANTES...Porque Música y sus compañer@s tuvieron un Gesto de Impotencia ante la sordera de la ministra y el Gobierno concertacionista-bacheletistaPorque las feministas autónomas no aceptamos la represión contra l@s jóvenesPorque las feministas autónomas creemos en el derecho de Tod@s a una Educación gratuita, digna y de calidad¡¡¡NOS VEMOS ALLÁ!!!
POR EL JARRAZO Y UNA EDUCACIÓN PÚBLICA GRATUITA Y DE CALIDAD PARA TODOS Y TODAS
Matemático ULTRA modesto !!!!!
sábado, 26 de julio de 2008
Uno de olimpiadas - Somachi (Olimpiadas Chilenas)

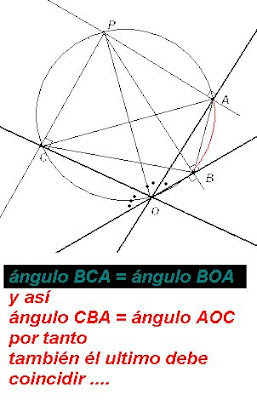
Tracemos la recta OP. Pensemos en la circunferencia que tiene por diámetro OP.
Esta circunferencia debe contener a los tres PUNTOS A, B, C, porque son pies de perpendiculares. Pues si el ángulo que subtiende un diámetro, es de 90º, el vértice del ángulo de 90º debe estar en la semicircunferencia que determina el diámtero. Esto se ve para los tres puntos A, B, C en este caso:
 Luego, al interior de esta circunferencia, es facil comprober lo pedido, pues los ángulos a comparar como iguales subtienden los mismos arcos .... veamos un ejemplo en el dibujo:
Luego, al interior de esta circunferencia, es facil comprober lo pedido, pues los ángulos a comparar como iguales subtienden los mismos arcos .... veamos un ejemplo en el dibujo: