Problema: Dadas 3 rectas en el plano, que concurren en el punto O , considere los 3 ángulos consecutivos que se forman entre ellas (cuya suma es, naturalmente, 180 grados). Sea P un punto del plano que no se encuentra en ninguna de las rectas y sean A , B , C los pies de las correspondientes perpendiculares trazadas desde P a cada recta. Demuestre que el triángulo ABC tiene los mismos ángulos que los que las rectas forman entre sí.
Solución: Representemos la situación:
Tracemos la recta OP. Pensemos en la circunferencia que tiene por diámetro OP.
Esta circunferencia debe contener a los tres PUNTOS A, B, C, porque son pies de perpendiculares. Pues si el ángulo que subtiende un diámetro, es de 90º, el vértice del ángulo de 90º debe estar en la semicircunferencia que determina el diámtero. Esto se ve para los tres puntos A, B, C en este caso:
Luego, al interior de esta circunferencia, es facil comprober lo pedido, pues los ángulos a comparar como iguales subtienden los mismos arcos .... veamos un ejemplo en el dibujo: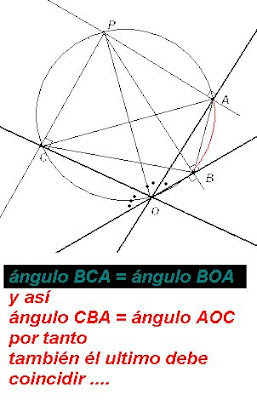
No hay comentarios:
Publicar un comentario