
Nivel: Enseñanza Media, Tercero año Medio.
CMO 2do. Medio: Regla de Laplace, para (micro)eventos equiprobables.
Contenido Extraordinario Tercero Medio: Grafica de regiones planares.
- - - - -
Se puede mirar en este BLOG lo que son los espacios enumerables y no enumerables, a propósito de varios posteor en torno a Cantor (Creo que uno le llamé, copiando un libro: El paraíso de Cantor) .... Pero recordemos algo:
El conjunto de los números pares y el de los impares son INFINITO enumerables puesto que vada uno de sus componentes se puede asociar a uno de los números naturales .... Pero el Conjunto de los números Reales (IR) no es enumerable, no se le puede asociar biunivocamente cada uno de los números naturales, ni si quiera el trazo [0,1] es enumerable, es tan infinito como el conjunto de todos los Reales (hemos puesto algunas imágenes visuales de ello) ....
Para la enseñanza media, se postulan probabilidades invocando conjuntos INFINITOS no enumerables, pero asociados a medidas geométricas finitas tales como LONGITUD, AREA y VOLUMEN.
Así las probabilidades de un evento A serán, en su fórmula Laplaceana:
P= Longitud de A / Longitud de S
P= Area de A / Área de S
P= Volúmen de A / Volúmen de S
Y en general se habla de que este tipo de probabilidades es uniforme.
Un BELLO ejemplo (no fácil):
Sobre la línea R (Reales), se selecciona al azar los puntos a y b tales que -2 <=b<=0 y 0<=a<=3 como se muestra en la figura. Hallar la probabilidad p para que la distancia d entre a y b sea mayor que 3.
CMO 2do. Medio: Regla de Laplace, para (micro)eventos equiprobables.
Contenido Extraordinario Tercero Medio: Grafica de regiones planares.
- - - - -
Se puede mirar en este BLOG lo que son los espacios enumerables y no enumerables, a propósito de varios posteor en torno a Cantor (Creo que uno le llamé, copiando un libro: El paraíso de Cantor) .... Pero recordemos algo:
El conjunto de los números pares y el de los impares son INFINITO enumerables puesto que vada uno de sus componentes se puede asociar a uno de los números naturales .... Pero el Conjunto de los números Reales (IR) no es enumerable, no se le puede asociar biunivocamente cada uno de los números naturales, ni si quiera el trazo [0,1] es enumerable, es tan infinito como el conjunto de todos los Reales (hemos puesto algunas imágenes visuales de ello) ....
Para la enseñanza media, se postulan probabilidades invocando conjuntos INFINITOS no enumerables, pero asociados a medidas geométricas finitas tales como LONGITUD, AREA y VOLUMEN.
Así las probabilidades de un evento A serán, en su fórmula Laplaceana:
P= Longitud de A / Longitud de S
P= Area de A / Área de S
P= Volúmen de A / Volúmen de S
Y en general se habla de que este tipo de probabilidades es uniforme.
Un BELLO ejemplo (no fácil):
Sobre la línea R (Reales), se selecciona al azar los puntos a y b tales que -2 <=b<=0 y 0<=a<=3 como se muestra en la figura. Hallar la probabilidad p para que la distancia d entre a y b sea mayor que 3.
 Solución:
Solución: La solución a este problema viene dado por el set de Inecuaciones que lo caracterizan. Tres son las inecuaciones:
-2 <=b<=0
0<=a<=3
d=a-b > 3
Veamos la región planar de pares ordenados Posibles:
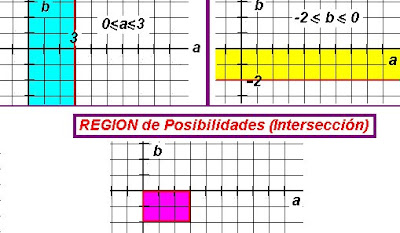
Está dada por todos los pares ordenados que cumplen las restricciones para a y b: -2<=b<=0 ; 0<=a<=3
Veamos ahora los pares ordenados de la región favorable, dados por la región que describe la inecuación d=a-b>3

Probabilidad Pedida=

No hay comentarios:
Publicar un comentario