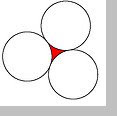
Partimos de tres circunferencias iguales. Las colocamos de forma que las tres sean tangentes entre si, es decir, cada una es tangente a las otras dos. Entre ellas queda una porción del espacio, que en la imagen está coloreada de rojo. El problema consiste en calcular el área de dicha porción del espacio sabiendo que el diámetro de cada una de las circunferencias es 10.
Respuesta: ya viene y no es tan difícil !
Considere que el triángulo que une los centros de las tres circunferencias es EQUILÄTERO de lado 2r. Cada uno de sus lados lo forman dos radios unidos, en línea recta, en los puntos de tangencia .... No olvidemos que el ángulo de un triángulo Equilátero es de 60º.
Muchas veces en este blog hemos calculado la altura de un triángulo equilátero correspondiendo a la mitad de su lado por raiz de tres .... (Hagan click en las etiquetas)
Miremos estos acuerdos en la siguiente figura:
Luego el área roja será:
(Area del Triángulo Equilátero Total) menos (TRES veces el área Amarilla (trozo torta))
Ojo que el área del trozo de torta es (60º/360º) el área del círculo !!!! La sexta parte, Veamos:
Uds. pueden ponerle los valores concretos a este cálculo genérico ....


No hay comentarios:
Publicar un comentario