viernes, 31 de julio de 2009
Las matemáticas son un lenguaje UNIVERSAL
una gran amiga !
una gringa más chilena que los porotos
(Alemana de Alemania)
me preguntó cómo era que:

 (llamemos a este recuerdo Definición Fundamental)
(llamemos a este recuerdo Definición Fundamental)
-
Decía y era cierto "que no andaba tan perdida, que algo recordaba" .... pero que esa cosa de más arriba era CHINO mandarín ...
-
Primero le dije que si a lo que sabía agregábamos la definición de factorial y otra Propiedad de las Potencias (Potencia de Potencia), era suficiente para entender por qué 64 se podía escribir de esa forma tan churumbélica ...
1) Veamos lo que es el factorial:
Se define el factorial como sigue:
n ! = n x (n-1) x (n-2) x ...... x 5 x 4 x 3 x 2 x 1
n ! se lee como "ene factorial" y con unos ejemplos queda muy fácil ...
6 ! = 6 x 5 x 4 3 x 2 x 1 = 720
5 ! = 5 x 4 x 3 x 2 x 1 = 120
4 ! = 4 x 3 x 2 x 1 = 24, etc.
2) Veamos la Propiedad Potencia de una Potencia:
La nueva potencia esta elevada al producto de los dos exponentes .... sigamos
=========================
Trabajemos entonces la expresión china de la izquierda, un poquito ....
 Luego sigamos, usemos lo que recordamos:
Luego sigamos, usemos lo que recordamos:
Queda demostrado entonces que 64 se puede escribir de esa forma tan alambicada ...
Estamos de acuerdo con la "Alemana Salvaje", o sea es que las matemáticas son quizás el único lenguaje universal ....
-
En otras cosas no estoy (estamos) de acuerdo con ella,
-
en como se escribe su apellido
en como suena el ladrido de los perros, ella dice que DRUF-DRUF, naquembeque, NO puede ser, por eso no nos entendemos con el 1er mundo! .... suena "GUAU-GUAU" o si no mi mamá me engañó a los 3 años!
y en como se come un helado PANDA en la calle !
En matemáticas ella es chilena y yo italiano!
jueves, 30 de julio de 2009
Robótica Escolar - Reporte en Terreno ....
Fue en una Universidad
Encuentro Interescolar de Robótica
Con la presencia de "Lego" y su división de Robótica
Yo fui con mi hijo, que desde hace mucho tiempo me dice que quiere construir un ROBOT
- es impresionante las variantes de construcción: Piñata Robot, Alcancía Robot, Robot verdadero-
El dice que los robot vienen con regalos, algo así como lo que nosotros llamamos FUNCIONES robóticas ....
Había 2 salas: una comercial y otra de competencia escolar
En la comercial, le dejaron manobriar un robot, usar sus controles
fue feliz, pero los robots =aplicaciones escolares= valen como de 105.000 pesos hacia arriba !!!
UFFFFF!!!!!
Y miramos las competencias y vimos lucir y deslucir ojos de niños y niñas de primero medio
sus profesores(as) acompañantes esforzándose por acompañar
y los robots subir la rampa y volcarse
unos programados por distancia
otros programados con sensores de color o de obstáculos
era maravilloso y a mi se me metió el bicho de la robótica
=las cosas en que lo involucra un HIJO=
el cuento era más o menos así:

y veamos un verdadero ROBOT

IO ROBOT ¡!
BIENNNNNNN !!!!!!!!!!!
miércoles, 29 de julio de 2009
martes, 28 de julio de 2009
Un ejercicio de Básica - SIMCE

Respuesta:

Qué es una Variable Aleatoria ?
I) Una variable discreta es aquella que toma infinitos valores.
II) Una muestra de una población no se debe escoger al azar.
III) Una variable continua es aquella que toma un conjunto finito de valores.
A) Sólo I
B) Sólo II
C) Sólo I y III
D) Sólo II y III
E) I, II, III
Solución:
Vamos a analizar cada una de las tres proposiciones:
Análisis de I) Una Variable Aleatoria Discreta es aquella que puede tomar solo un número limitado de valores numerables. De otra forma, se dice que una variable es discreta, si su recorrido es discreto, lo que se contradice con "tomar infinitos valores". Esta proposición es FALSA.
Análisis de II) Si no se escoge al azar, habrá un criterio de elección que hace que la muestra esté sesgada en torno a ese criterio. Una muestra, para ser VERDADERAMENTE REPRESENTATIVA, DEBE ser al azar.Imaginemos preguntar por una candidatura presidencial en un sólo estrato social, esto sesgaría la muestra y NO lograría ser verdaderamente representativa.Esta proposición es FALSA!
Análisis de III) Una variable aleatoria continua es aquella que puede tomat cualquier valor dentro de un intervalo dado de valores no numerables. Dicho de otro modo, el conjunto de valores de la variable abarca todo un intervalo de números reales. Para el caso de la estatura, que es una variable continua por ejemplo entre 0 y 2,5 metros (por poner dos cotas)- las estaturas posibles que se pueden escoger en este intervalo son infinitas. Esto contradice lo de "toma un conjunto finito de valores". Esta proposición es FALSA!
I) , II) , III) son FALSAS, Alternativa E)
lunes, 27 de julio de 2009
Teorema de las Secantes - Completando el Diccionario
Campeonato Mundial de Memoria Rápida
Los memoriones del planeta compiten por el título 2009
Sólo mañana, en la final, y tras superar una serie de pruebas (ver recuadro) y a otros 20 competidores, el español Ramón Campayo (44) sabrá si logró su objetivo. "Mi intención es batir por lo menos tres de los siete récords posibles", ha dicho, seguro de sí mismo. Y de su memoria.
No por nada lleva invicto tanto tiempo y es invitado permanente a programas de televisión donde ponen a prueba su gracia: recordar perfectamente el orden de 6 mazos de cartas, la ubicación de 84 fichas de tres juegos de dominó, los precios de un pasillo repleto de mercadería en un supermercado, o las patentes de 20 autos que pasan por la calle.
Incluso, ha sido capaz de memorizar una cadena de 23.200 palabras -que le fueron dichas una a una durante 72 horas y una sola vez- recordando la posición exacta de cada una.
Y él, como si no se esforzara. Es el resultado de una habilidad innata y de un perseverante entrenamiento.
Desde chico se sintió atraído por el mundo de la mente, según comentó a la agencia EFE. "Inventaba, a modo de juego, técnicas que me sirvieran para estudiar mejor en el colegio, y pronto vi que me servían, y empecé a tomármelo en serio".
Sin embargo, no fue sino hasta 2003 que Campayo empezó a interesarse por las pruebas de memorización rápida y comenzó a competir, precisamente en Münich, ciudad donde batió, de una sola vez, 15 récords del mundo.
Aunque su fama se ha extendido por todos los continentes y se le considera una de las mentes más privilegiadas de la historia, muestra una actitud modesta: "Lo primero es la confianza y, para mí, mi mente es mi amiga".
Fuera de las competencias, la mayor parte de su vida pasa en la escuela de memoria que él mismo administra en España, y en la que dicta cursos de técnicas de estudio para niños y adultos.
Además, su cerebro prodigioso ha suscitado el interés de los científicos sobre cuánto de su habilidad es innata y cuánto es sólo entrenamiento, lo que podría ayudar al tratamiento de trastornos de la memoria.
Funes el memorioso (J.L. Borges; un cuento muy matemático)
Raíces .... un pequeño desafío de Racionalización



domingo, 26 de julio de 2009
Delirios Matemáticos: Cuento I V
Y esta vez
puedo contarles como llegué a ser el "primer guerrillero de las matemáticas"
Y antes que este año me lo haga perder todo
-y ante la cruda situación laburo-
salí a las calles,
esta vez NO para marchar
sino para propagandear mi blog de Mates - de la psu-mates
pintándole por las paredes
le tocó al Metro Macul
y estaba en lo mejor cuando
el guión de al medio: psu-matematicas
se convirtió en punto abajo: psu.matematicas
y luego en la deseperación
pasó a ser un guión bajo: psu_matematicas
y luego un guión al medio
que produjo algo así como un igual: psu=matematicas
(lo que es una ecuación falsa, valga de paso)
a la conchemimura!
terminé enojado y enrabiado el pintarrajeo
y volví a la casa
a cortar un papelito del tamaño
y a buscar neoprene, con las mano todas neuras (negras quiero decir)
y volver
cagado de frío
-cual quijote gordo- a arreglar el entuerto
por lo menos uds.
no se equivoquen:
http://psu-matematicas.blogspot.com/
y nunca podrán decir
...
que
NO
amo
a
los
hijos
....
(cuento IV, publicado en la perra de la calle)
viernes, 24 de julio de 2009
jueves, 23 de julio de 2009
Vértice de una Parábola
Qué nos enseña el Discriminante en la Función Cuadrática?
Ejemplo:
En la siguiente Ecuación de Segundo grado el discriminante es negativo y efectivamente las raíces son complejas conjugadas ,,,,, veamos:
Sobre Evaluaciones

Comentario de la evaluación
1. La grafía del signo seis es del todo correcta.
2. Se puede apreciar lo mismo con el siete.
3. El signo más nos dice, acertadamente, que se trata de una suma.
4. En cuanto al resultado vemos que el uno es correcto. El segundo número, efectivamente, no es ocho. Bueno, si lo cortamos por la mitad de arriba abajo, observamos que el alumno ha escrito dos treses simétricos. Elegimos el bueno porque se ve que su intención era buena.
El conjuntode estas observaciones evidencia que:
(a) La actitud del alumno es positiva (lo intentó)
(b) Los procedimientos son correctos (los elementos están ordenados correctamente).
(c) En conceptos sólo se equivocó parcialmente en uno de los seis elementos que forman el ejercicio. Esto es casi de sobresaliente.
En Consecuencia podemos otorgarle un "Notable" y decir que "Progresa Adecuadamente"
Emoción .... Hawking sobre las preguntas esenciales en el UNIVERSO
OJO: que se pueden elegir los SUBtítulos en Español ....
Humor Matemático ....
La señorita K - - - - - - - - - - (intento de cuento)

No sé si la señorita K tiene 14 o 15 o 16 años, algo así.
Yo soy el profesor Chungungo o señor C.
Soy APRENDIZ de Educador en el área de Matemáticas.
(Soy de los que cree que uno nunca supera el estado de APRENDIZ)
Este cuento se llama:
-
"La señorita K" ó en un remedo burdo de otro título en inglés, también le llamo:
"Teachers who loves to much"
-
No la amo a ella, por cierto!
Pero amo enseñar, aunque a veces dudo.
La señorita K es hija de la Señorita F.
Yo -y aquí está mi error-
ofrecí por lazos familiares, ayudar cuando fuera necesario a la señorita K con sus guías, pruebas y en general con los entendimientos del grado que cursa, un maestro chasquilla, un soporte en línea, online ...
Siempre como que soy yo el que me ofrezco.
A la menor dificultad,
ya estaba sugiriendo ayudarle a completar la guía, poniendo fecha, reparando mis saberes. Traje andamios, cochallullos y un compaz.
La señorita K dijo: "no creo que esta materia sea tan importante para el exámen"
y puso esta condición, esta fianza, este augurio ....
al final vimos someramente el espíritu de la materia
-nada de esfuerzos- .... luego,
La señorita F me dijo: "vamos a revisar lo de las clases porque en esos días ella llega tarde, cansada".
Y al final me pasó otra vez:
tengo yo más emoción que mis estudiantes !
¿ puede uno enseñar a un(a) otro(a) que no quiere aprender ?
-
En el viejo y popular sector de LH
enseñé en cursos de recuperación del Ciclo Medio.
Yo era el único que llegaba temprano, arreglaba la sala, hacía el aseo, ponías las mesas, limpiaba la pizarra .... todos y todas llegaban tarde, con sus mochilas, tras servir la cena a sus parejas ....
Estaban cansados es cierto!
Pero nunca supe si logré traspasar la imperiosa o amorosa necesidad de una "paideia holística -no clasista como la Paideia Griega-" para el siglo que vivimos ....
por eso digo que soy APENAS:
un
viejo
APRENDIZ
de
educador,
enamorado
precoz (sobretodo precoz)
intenso
que
no
encuentra
alguien (un otro o una otra)
que,
escapando
del
reggeatton y las tarjetas,
se
sitúe
en
la
antípoda
para
amar ... (no se espante!)
...
para
amar
estudiar ....
miércoles, 22 de julio de 2009
Una pirámide MUY esotérica .... (cosas de Horodoto)
Veamos una pirámide muy especial, señalada ya por Herodoto, como una con poderes ....
Dice Herodoto que
" la altura del triángulo debe estar en proporción áurea con la mitad de la base. "
construyamos:
Sea x el apotema (la altura de cada cara).
Y sea la base de cada triángulo igual a 2.

Y Herodoto dice que la altura del triángulo debe estar en proporción áurea con la mitad de la base:
(altura del triángulo)/(mitad de la base) = (x)/1 = fi. (radio áureo)
=====
Nota Esotérica: dicen que si uno pone una hoja de gillete al interior de una pirámide con estas mediciones, esta no pierde o incluso recupera el filo .... que los alimentos NO se descomponen y qué esperar si uno medita dentro de una de ellas !!!!
Apuesto que te da 34 .... MAGIA-JUEGOS ....

lunes, 20 de julio de 2009
Repunte en el SIMCE
Concretamente, en la última prueba Simce de 4° básico, aplicada el año pasado, los colegios de dichas comunas que trabajaron con el programa de Arquimed subieron sus promedios 20 puntos respecto de la evaluación de 2007.
En terreno
"Llevamos muchos años como proveedores de materiales didácticos y tecnologías educativas. Pero en 2006 vimos que los colegios invertían en esto, pero finalmente el impacto era bajo. Algunos ni siquiera usaban en el aula estos recursos", cuenta Sebastián Miranda, director de servicios educativos de la firma.
Por eso armaron una estrategia de asesoramiento a las escuelas, formando un equipo de monitores que van con los docentes a las aulas y les ayudan a hacer clases más atractivas. "El objetivo era romper el modelo de clases expositivas y que los protagonistas sean los alumnos. O sea, lo que todos dicen que hay que hacer, pero que muy pocos hacen de verdad", dice Miranda.
La clave es el modelaje en aula; es decir, que la capacitación de los profesores se haga en terreno, en sus salas y con los mismos niños con que trabajan a diario. Son dos horas a la semana de apoyo, y dan frutos. "Tomar a los docentes y llevarlos a capacitaciones a una universidad no sirve. Cuando el monitor está con ellos en su sala es diferente, es una capacitación aterrizada a sus necesidades concretas", plantea Sandra Ergas, directora de proyectos de Arquimed.
Así, los profesores logran hacer clases de ciencias, lenguaje y matemática marcadas por el trabajo grupal y la experimentación de los alumnos.
Dados los resultados, desde 2008 Arquimed decidió ofrecer asistencia técnica externa a los colegios que reciben la subvención escolar preferencial. Hoy trabajan en 295 escuelas, atendidas por 120 monitores.
Además de puntos en el Simce, el método ha cosechado reconocimiento entre los expertos. En 2008, País Digital lo señaló entre las 50 iniciativas de innovación educativa "made in Chile". Por lo mismo, Arquimed está trabajando con tres universidades: con la Arturo Prat existe un convenio para formar a sus egresados de pedagogía como monitores, con la Usach realizarán un diplomado a partir de agosto y con la Católica de Temuco trabajan para incluir una asignatura sobre su método en la formación de docentes y para realizar investigación sobre el modelaje en aula.
LOS PILARES
sábado, 18 de julio de 2009
La regla extraña del Dr. Matrix
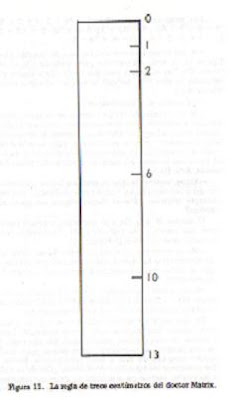
Formar los números del 1 al 20, con cuatro números 4 y las operaciones básicas ....
Sumas
Restas
Divisiones
Multiplicaciones
Factorial
Raiz
Potencias
Paréntesis
el punto que puesto arriba de 0,4 es 0,4444444 .... (periódico)
la coma para los decimales
el cero antes de la coma decimal NO se cuenta.
1=
2=
3=
4=
5=
6=
7=
8=
9=
10=
11=
12=
13=
14=
15=
16=
17=
18=
19=
20=
Demos un ejemplo: 1 = (4x4)/(4x4) .... y los otros ?


Un poco más difícil ....
con cuatro números cuatro (más o menos complicado)
con tres números cuatro (más sencillo)
con sólo dos números 4 (más complicado)
=============================================
(Nota 1: Este último NO lo pude resolver y busqué la respuesta)
(Nota 2: Tomado del libro de Martín Gardner: Los mágicos números del doctor Matrix)
jueves, 16 de julio de 2009
y qué pondrías tú si debieses enviar un mensaje al espacio para detectar vida ?
Las siguientes tres páginas están cifradas en un lenguaje artificial, Lincos, diseñado por el Doctor en Matemáticas Hans Freudenthal con la intención de crear un lenguaje universal capaz de hacer posible la comunicación con especies extraterrestres totalmente diferentes, Lincos utiliza la matemática y la lógica serial como patrón universal de partida.
-
Los integrantes del proyecto Cosmic Call enviaron un mensaje hacia las estrellas más cercanas a la Tierra, por radio telescopio durante el verano de 1999. Otro mensaje fue enviado en 2003. La fuente de envío, fue un telescopio de 70 metros de diámetro preparado para enviar mensajes localizado en Ucrania.
-
El mensaje de 1999 constaba de 23 páginas con símbolos extraños ....
a continuación mostraré tres páginas (que en todo caso no son las tres primeras páginas de los emnsajes enviados) y te pedimos que trates de imaginar qué contenidos se vierten en cada una de ellas:
Uno:
 Dos:
Dos:
Tres:

Ahora explicaremos algunos de lo selementos de estas tres páginas ...
INTENTA IMAGINAR ....
Página 1:

Página 2: A simple ojo está la circunferencia y el círculo,está marcado el diámetro, va el valor de Pi y más abajo el Teorema Particular de Pitágoras .....
Página 3: Esta es lamássencilla,en ella se expone la talla delos seres humanos,su aspecto externo y un promedio de su longitud ....
Mira que maravilla el texto completo en (PDF): : http://www3.sympatico.ca/stephane_dumas/CETI/messages.pdf
miércoles, 15 de julio de 2009
En topología, una botella de Klein es una superficie no orientable cerrada de Característica de Euler igual a 0 que no tiene ni interior ni exterior. Fue concebida por el matemático alemán Christian Felix Klein, de donde se deriva el nombre.
Se puede obtener una representación tridimensional de una Botella de Klein introduciendo el extremo delgado de una botella o de un matraz a través de uno de los lados del recipiente y uniéndolo a la base. Hay que recalcar que dicha representación no es una Botella de Klein. Físicamente puede ser realizada sólo en un espacio de cuatro dimensiones, puesto que debe pasar a través de sí misma sin la presencia de un agujero.
martes, 14 de julio de 2009
¿Crees en la numeralogía y esas yerbas?

lunes, 13 de julio de 2009
¿Cómo vamos en CIENCIAS?
a) Antiácidos; b) Cortisona ; c) Aspirina.
2.) Según la mayoría de los astrónomos, ¿Cuál de los siguientes ya no se considera un planeta?
a) Neptuno ; b) Plutón ; c) Saturno ; d) Mercurio.
3.) ¿Cuál de las siguientes es una causa de tsunami?
a) Una corriente oceánica muy cálida ; b) Un gran cardumen de peces ; c) El derretimiento de un glacial ; d) Un terremoto bajo el océan0.
4.) ¿Qué requiere el sistema de posicionamiento global o GPS para funcionar?
a) Satélite ; b) Estrellas ; c) Magnetismo ; e) Láseres.
5.) ¿Qué gas la mayoría de los científicos cree que provoca un alza de la temperatura de la atmósfera?
a) Hidrógeno ; b) Helio ; c) Dióxido de carbono ; d) Radón.
6.) ¿En qué se diferencian las células madres de las otras células?
a) Se pueden convertir en distintos tipos de células ; b) Se encuentran sólo en la médula ósea ; c) Se encuentran sólo en las plantas.
7.) ¿Qué han descubierto recientemente los científicos en Marte?
a) Platino ; b) Plantas ; c) Hongos ; d) Agua.
VERDADERO o FALSO:
8) Los continentes se han estado moviendo por millones de años y continúan haciéndolo.
9) Los láser funcionan concentrando ondas de sonido.
10) Los antibióticos matan a virus y a bacterias.
11) Los electrones son más pequeños que los átomos.
12) Toda radiación es originada por el hombre.
===========================
RESPUESTAS en los COMENTARIOS
Nota: Este es un extracto de una encuesta que se utilizó en USA para ver como anda la gente en conocimiento científico.
sábado, 11 de julio de 2009
Un problema geométrico (de Gaussianos)
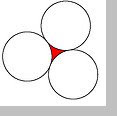
Respuesta: ya viene y no es tan difícil !
Considere que el triángulo que une los centros de las tres circunferencias es EQUILÄTERO de lado 2r. Cada uno de sus lados lo forman dos radios unidos, en línea recta, en los puntos de tangencia .... No olvidemos que el ángulo de un triángulo Equilátero es de 60º.
Muchas veces en este blog hemos calculado la altura de un triángulo equilátero correspondiendo a la mitad de su lado por raiz de tres .... (Hagan click en las etiquetas)
Miremos estos acuerdos en la siguiente figura:
Luego el área roja será:
(Area del Triángulo Equilátero Total) menos (TRES veces el área Amarilla (trozo torta))
Ojo que el área del trozo de torta es (60º/360º) el área del círculo !!!! La sexta parte, Veamos:
Uds. pueden ponerle los valores concretos a este cálculo genérico ....
viernes, 10 de julio de 2009
Savater .... profeta ! (Blog Bezmiliana, linkeado en los favoritos)
Y si Newton no fue ....
Una escuela poco conocida de estudiosos en el sudoeste de la India descubrió uno de los principios fundamentales de las matemáticas modernas, alrededor de tres siglos antes que Newton, según una nueva investigación. George Gheverghese Joseph, de la Universidad de Manchester, afirma que la Escuela de Kerala identificó las “series infinitas” (uno de los componentes básicos del cálculo) en el siglo XIV.

El descubrimiento se atribuye actualmente en los libros a Isaac Newton y Gottfried Leibnitz, a finales del siglo XVII.
El equipo de las universidades de Manchester y Exeter ha revelado también que la Escuela de Kerala descubrió cómo trabajar con la serie de Pi y calculó esta constante con 9, 10, y finalmente 17 decimales.
Existen fuertes evidencias circunstanciales de que los hindúes divulgaron sus descubrimientos matemáticos a los misioneros jesuitas expertos que visitaron la India durante el siglo XV. Ese conocimiento, sostienen los autores del estudio, pudo acabar siendo transmitido al propio Newton.
- (Tomado del blog Bezmiliana)-
Más información: http://www.electronicafacil.net/ciencia/Article11002.html
-
Una mesa de billar perfecta .... (Club Bezmiliana)
Vídeo realizado por el Club Científico Albert Einstein del I.E.S. La Rosaleda de Málaga.
jueves, 9 de julio de 2009
Un árbol se compone de árboles pequeños ....
Entrevista a Benoît Mandelbrot: suavidad, rugosidad y fractales
Para saber más de Benoit Mandelbrot, mirar en WIKIPEDIA:
Una duda sincera de profesor que aprende y que quiere aprender cada día, en concreto de sus propias dudas ....
Preguntas a los y las colegas profesores(as) ....
¿Quién puede comentar este ejercicio?

entonces, la primera expresión que representa un número racional es:

Tomado de: Proyecto SER - Santillana - 2007
Comentarios en cuanto a la construcción del enunciado y en relación a las respuestas que entrega .... ESTO ES MUY INTERESANTE !!!!
Comentario: Este ejercicio NO lo voy a resolver acá. Está resuelto en el nuevo BLOG especializado en PSU:
http://psu-matematicas.blogspot.com
Pero si lo vamos a comentar .... es muy curioso, incluso creo que no es una buena formulación o es bien visionario o innovador ....
Posee dos alternativas correctas: D) y E).
Pero fíjense que dice en su enunciado: "la primera expresión que representa un número racional es", por tanto, la respuesta debiese ser D).
Esto puede llevar a confundir a los estudiantes y NO es plausible que un ejercicio lleve a confusiones.
En todo caso, no sólo habría que realizar las prueba de las alternativas sino que seguir bien el protocolo señalado en la pregunta .... casi como que hay entremedio la comprobación de si el(la)educando es capaz de "SEGUIR una SEÑAL ÉTICA".
OJO: mucha gente -en la que me incluyo- responde mirando las alternativas NO en orden. Buscando en un vistazo encontrar la respuesta .... eso muchas veces lo hago y triunfo .... ¿ Qué pasa si uno lee las alternativas al revés ????? Porque no es obligatorio leer de arriba hacia abajo!!!!
Entonces, al leerlas al revez, de inmediato habría marcado la letra E)
OJO con este ejercicio, señores del Proyecto SER.














